Geometric signal interpretation of complex exponential oscillators

   

Following from my last post on geometric interpretation of complex numbers, I looked for a clear explanation of complex exponentials.

The model of complex exponentials:

a = a ejA = a cos(A) + j * a sin(A)

lets us use complex arithmetic to do things with vectors.

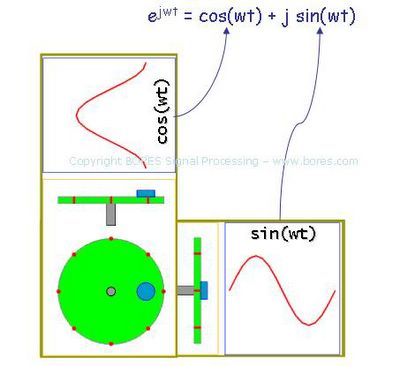
To see how this can be used to model real signals, think about a rotating wheel with a knob on. I found a nice animation of this by Jim Lesurf of the University of Saint Andrews which has a nice beach (though very cold) and a famous golf course nearby. His animation is at:

http://www.st-andrews.ac.uk/~www_pa/Scots_Guide/info/signals/complex/cmplx.html

and I borrowed his pictures (with permission) to use in the slide I generated (an extract from which is shown above).

If we look at the wheel from the front, we can see that the motion of the knob is circular. But if we look from the side, it looks as though the knob just goes up and down - and if we plotted its up- and down-ness against time this would be a sine wave.

Think for a moment, and realize that we cannot tell from the side whether the wheel is rotating clockwise or counter-clockwise - so we have lost some information by only looking from one side (and this must be a Bad Thing). Also, sometimes we measure only small displacements of the knob in the up and down sense - and if there were also noise signals then sometimes the signal may be buried in the noise - so we can infer that we have lost some signal-to-noise ratio too.

We can recapture all the information by realizing the signal is 2D and so we can fully represent it by a 2D vector, drawn from the center of the wheel to the knob - and this vector can of course be represented by a complex number. Now we will see two sine-like waves - a sine wave from one side, and a cosine from the other - and can plot the circular path.

Suppose the vector is a, and the angle of the wheel at time t is (wt), then the knob’s position at time t can be represented by the vector:

a ejA = a cos(A) + j * a sin(A)

If the wheel were replaced by some kind of eccentric crank, or by a complex system of gears, we would still be able to fully reconstruct the path but of course the component signals would not be simple pure sine and cosine waves.

Taking it further, imagine a rotating bar magnet with two coils at right angles: the magnetic fluc willcross the coilds and generate sine and cosine currents in each. Of course the bar magnet could be the magnetic vector of a radio photon, in which case we have a nice model of quadrature RF detection coils.

So complex exponentials give us a nice way to model oscillators.

Comments

Post a Comment

Popular posts from this blog

Bread and cocktails

A cocktail has as many calories as half a loaf of bread. This is the kind of statistic The Meejah love. How many calories are there in half a loaf of bread? What sized loaf? What kind of bread? What sort of cocktail? I am left bemused by this kind of statistic, which is almost but not quite totally devoid of meaning. It is what I would call a 'factoid': a fact that is at the same time surprising, seemingly dodgy, but probably - within its own logical scope - true in a sense. Actually it isn't a real factoid - a factoid is epitomised by my son James's factoids, which are totally true, quantitative, specific facts that are, however, surprising either in being contrary to what one expects or (better, for a good factoid..) just the sort of fact you never thought you would ever need to know or wish to know. James is, and always has been, good at factoids: a photographic memory combined with attention to what most of us ignore equips him to store factoids, and is...
Read more

Wave Watching

A few years back I found oceanographer Mirjam Gleesmer’s blog ‘Wave Watching’: https://mirjamglessmer.com/wave-watching/ which is just what it says: a fascinating and insightful blog about watching waves – and what we can learn from doing so, not only about waves but about what they traversed, reflected off, diffracted around, broke over… It spoke to me particularly because I was then watching waves almost obsessively: ripples on puddles, waves on our local lake, splashes from moorhens and coots and ducks on the canal; sea waves, coastal waves, every kind of wave. I wouldn’t quite say it risked losing me friends but people certainly got used to walking on and eventually looking back surprised to see me stopped staring at some interesting wave phenomenon. Although I became interested in those sorts of waves they weren’t the source of my interest: radio wave were. I’ve studied and worked with waves a lot: it’s a foundation topic in physics and electronics, and I’ve worked on soun...
Read more

Homeschool maths

Homeschooling has become a household word during pandemic lockdown, but both my grandchildren have been homeschooled since before the pandemic. Surrey historically has too few state school places, and Joshua was not offered one locally so would have had an hour's commute to a school in the next town. My daughter Jenny runs a pre-school and has a good educational brain, so took the brave - and so far very good - decision to homeschool. Since they all live with us (we are what in pandemic times is called a 'multigenerational household') I get to see homeschooling in action. Although I spent much of my career teaching, it was in industry and at Masters university level so I am involved mostly in opining wisely about strategy rather than actually teaching school level. Since I studied physics and spent my career in physics, computing and mathematics I am handy to have around to answer questions but despite having been a school governor for ten years and chair of governors for f...
Read more