Geometric signal interpretation of complex numbers

   

In revising the slides and notes for our class Introuction to DSP, I decided to add some explanation of complex numbers and how they relate to the real world. This is important because we actually develop DSP math using complex numbers, although most often we explain it (informally) without recognizing this.

Using complex numbers is useful because the math works well, but is often difficult for people to understand in practical terms - that is, what does the complex number represent?

In fact, though, many signals are easier to deal with if we think of them as being ‘2-dimensional’ vectors. A vector has both length and direction (or, in an x/y coordinate system, two components - x and y).

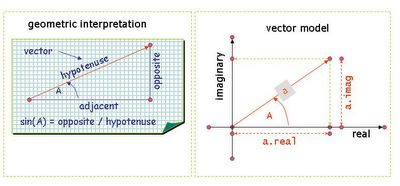
For example think of a sine function: at first sight this seems to be a classic case of a 1- dimensional signal - it has just one varying value (the sine). But a sine value is in fact derived from trigonometry, based on the ratio of the lengths of the sides of a right-angled triangle - the ‘opposite’ divided by the ‘hypotenuse’. So in some ways a sine is in fact better represented not just as some rather abstract number but as a triangle with an angle and a hypotenuse.

This leads us to the idea of treating the hypotenuse as a vector with length and direction (phase angle). A vector can be defined by its length and angle, or by specifying two (Cartesian, or ‘x, y’) components at right angles. But it would be nice to have just one ‘number’ to represent the vector, instead of always having to deal with the x and y components separately. Complex numbers give us a way to define such numbers.

Complex numbers have two components, that correspond to the ‘x’ and ‘y’ components. These are called the ‘real’ and the ‘imaginary’ components. A complex number is defined as a single entity (or ‘number’) but that is calculated as the sum of its real and imaginary parts:

a = a.real + j * a.imag

where ‘j’ is ‘the square root of -1'.

Before we get agitated about a square root of a negative number - because we were taught at school that any number squared gives a positive - let’s remember that lots of things we were taught are not in fact so: your school teacher was wrong, and you can have a negative square. Anyway, we are doing engineering so we will just use a property of j, leaving the philosophy to the mathematicians. j has just one property: when squared, it is equal to -1. That’s it. Nothing else. It makes the math work in a useful way - as we shall see.This is simpler in the sense that we can now write our arithmetic (or computer code) as things like: c = a + b instead of writing out all the manipulations for the components separately.

Comments

Post a Comment

Popular posts from this blog

Bread and cocktails

A cocktail has as many calories as half a loaf of bread. This is the kind of statistic The Meejah love. How many calories are there in half a loaf of bread? What sized loaf? What kind of bread? What sort of cocktail? I am left bemused by this kind of statistic, which is almost but not quite totally devoid of meaning. It is what I would call a 'factoid': a fact that is at the same time surprising, seemingly dodgy, but probably - within its own logical scope - true in a sense. Actually it isn't a real factoid - a factoid is epitomised by my son James's factoids, which are totally true, quantitative, specific facts that are, however, surprising either in being contrary to what one expects or (better, for a good factoid..) just the sort of fact you never thought you would ever need to know or wish to know. James is, and always has been, good at factoids: a photographic memory combined with attention to what most of us ignore equips him to store factoids, and is...
Read more

Wave Watching

A few years back I found oceanographer Mirjam Gleesmer’s blog ‘Wave Watching’: https://mirjamglessmer.com/wave-watching/ which is just what it says: a fascinating and insightful blog about watching waves – and what we can learn from doing so, not only about waves but about what they traversed, reflected off, diffracted around, broke over… It spoke to me particularly because I was then watching waves almost obsessively: ripples on puddles, waves on our local lake, splashes from moorhens and coots and ducks on the canal; sea waves, coastal waves, every kind of wave. I wouldn’t quite say it risked losing me friends but people certainly got used to walking on and eventually looking back surprised to see me stopped staring at some interesting wave phenomenon. Although I became interested in those sorts of waves they weren’t the source of my interest: radio wave were. I’ve studied and worked with waves a lot: it’s a foundation topic in physics and electronics, and I’ve worked on soun...
Read more

Homeschool maths

Homeschooling has become a household word during pandemic lockdown, but both my grandchildren have been homeschooled since before the pandemic. Surrey historically has too few state school places, and Joshua was not offered one locally so would have had an hour's commute to a school in the next town. My daughter Jenny runs a pre-school and has a good educational brain, so took the brave - and so far very good - decision to homeschool. Since they all live with us (we are what in pandemic times is called a 'multigenerational household') I get to see homeschooling in action. Although I spent much of my career teaching, it was in industry and at Masters university level so I am involved mostly in opining wisely about strategy rather than actually teaching school level. Since I studied physics and spent my career in physics, computing and mathematics I am handy to have around to answer questions but despite having been a school governor for ten years and chair of governors for f...
Read more